Humboldtkurs Mathe-Krimi

Kursablauf

Das Wichtigste zu Beginn: Der Kurs überschneidet sich nur teilweise mit dem herkömmlichen Mathematikunterricht, vielmehr ermöglicht er andere, spannende und faszinierende Auseinandersetzung mit Besonderheiten der Mathematik.

Dazu werden wir anhand eines Mathe-Krimis von A. Beutelspacher die Rolle eines zwölfjährigen Jungen einnehmen und anhand von mehreren Kapiteln die Bedeutung, Schönheit und das z.T. Geheimnisvolle der Mathematik entdecken, überprüfen und ausprobieren.

Wir lösen aufgeworfene bzw. versteckte spannende Problem- und Fragestellungen als Kommissar, vervollständigen unsere Akte gemäß den Vorgaben der Kriminalakte. In der fächerübergreifenden Auseinandersetzung nutzen wir ein Lesetagebuch um unsere Erkenntnisse festzuhalten und lassen unserer Kreativität in Form von künstlerischen Interpretationen der Geschehnisse im Buch (Zeichnungen o.ä.), als auch im Erstellen von Hilfsmitteln der Mathematik (z.B. Caesar-Scheibe) freien Lauf.

Ein Auszug zu diskutierender Fragen ist folgend dargestellt:

• Wie erfolgt die Verschlüsslung von Nachrichten? Welche Techniken haben die Freimaurer früher angewandt? Was hat eine Caesar-Scheibe damit zu tun? Wie erreicht man eine gute Verschlüsslung?
• Inwiefern kann 1+1=0 gültig sein?
• Welche Besonderheit steckt in der Zahl pi? Wo kommt diese Zahl vor?
• Was ist eine alternierende Quersumme und was hat das mit der Teilbarkeit von 11 zu tun?
• Was ist eine vollkommene Zahl? Wie viele gibt es davon?
• Hat die Natur eine Ordnung? Fibonacci macht’s möglich!

Gemäß dem Zitat von Hans de Rijk ist ein übergeordnetes Ziel des Humboldtkurses eine authentische Begeisterung am Fach Mathematik.

„Sieh die Mathematik als einen wunderschönen Garten. Mitten in dem Garten steht ein gewaltiger Baum mit Ästen, die in den Himmel reichen. Mit dem Stamm des Baumes sind die Namen großer Mathematiker aus der fernen Vergangenheit verbunden: Pythagoras, Archimedes, Euklid. Höher im Baum finden sich die Namen kluger Köpfe wie Euler, Gauß und Hilbert. Will man die Mathematik ganz oben im Baum bewundern, dann muss man ganz schön klettern.

Aber der Garten besteht nicht nur aus Bäumen alleine; es gibt auch Blumenbeete und Sträucher.  An denen kann man sich auch ohne Klettern mindestens so erfreuen. Und ganz einfach auf dem Boden, zwischen dem Gras, steht manchmal ganz unerwartet ein wunderschönes Gänseblümchen.“ [1]


Bildergalerie:

1) Caesar-Scheibe für den Caesar-Code:

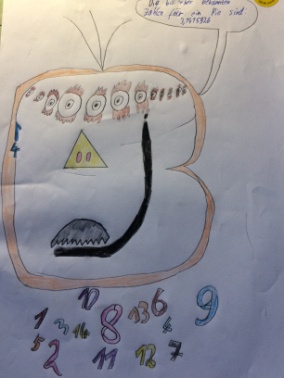
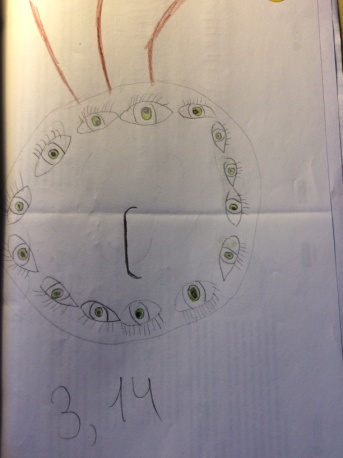
2) Eine Figur namens "Dreikommavierzehn":

3) Vorlage der Kriminalakte:
 


[1] Quelle: Kaenders, R. (2009): Antrittsvorlesung - Begeisterung für Mathematik, 2009. nach Swaen, M..(2006): De wiskunde van Hans de Rijk . Pythagoras, September 2006.